(元)支部長コラム其の10「50話補足：統計学を知ることがエッジになる！」

なさんこんにちは。坂本タクマです。久しぶりのコラムです。

今回は全シ連第50話の補足をいたします。すなわち、テーマは「統計学」です。ああ、みなさんの顔が浮かびます。私が昭和漫画史の話をするのを聞いているときの子供達のような顔が。

まあ確かに、統計学の学習はけっこう困難ではあります。用語がたくさん出てきてごちゃごちゃします。そういったものをひとつひとつ丹念に理解していく必要があります。個人的な経験から思うのは、ある知識が「役に立たない」と感じるのは、役に立つレベルにまで理解が深まっていないからであることが多い、ということです。

全シ連第50話で取り上げたのは、「期待値」という言葉です。これがなかなかの曲者です。システムトレーダーの間では、定着した用語として普通に使われていますが、厳密に追求するのはかなり大変です。

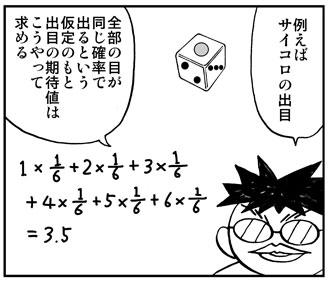
漫画の中で取り上げたサイコロのような例ならば、計算で簡単に求めることができます。計算で求められるのは幸いです。現実には、計算では求められない期待値もたくさんあります。トレーディングシステムの期待値もそのひとつです。

いや、サイコロでさえ、実はそう簡単ではないかも知れません。出目の期待値が3.5というのは、全部の目の出る確率が等しく6分の1であるという理想的なサイコロを仮定して計算したものです。現実に、あるひとつの「本物の」サイコロを持ってきて、その出目の期待値を求めるとしたらどうでしょう。本当に全部の面が等しい確率でしょうか。カジノで使うような高精度のサイコロであっても、ミクロのレベルで測定すれば、各面の面積がちょっとずつ違っているのではないでしょうか。たとえ完全に等確率なサイコロができたとしても、1度振れば、わずかに変形したり摩耗したりして、完全ではなくなるのではないでしょうか。

サイコロならば、そこまで深く考え過ぎなくとも「6分の1」ということで実用上はほとんど問題はないでしょう。しかし、相場は上等なサイコロよりはずっと変形しやすいもの、いわば粘土でできたサイコロのようなものですから、いくら考えても考えすぎということはないのではないでしょうか。なにしろ株式を発行する企業の経営者や社員は変わる、相場への参加者も変わる、取引所のルールまで変わってしまうのですから。

こう考えてくれば、ある売買戦略について、ひとつの固定された期待値が存在し、実トレードを続けていけばそれに収束していく、というのはまだ浅い理解と言いわざるをえないのではないでしょうか。期待値は移ろっていくもの、と考えるほうが自然な気がします。そういうものを期待値と呼んでいいのかは分かりませんが。

今までいろいろなトレーダーの方とお会いしてお話しをしてきましたが、その中の何人かの方が「あまりに昔のデータまで検証するのは意味がない」というようなことをおっしゃっていました。その真意は、上のようなことなのでしょう。

漫画の中には「大数の法則」という言葉も出てきます。標本数を増やすほどその平均は「真の平均」に近づいていく、という、統計学がよって立つ根幹です。これは数学的に証明されたものですから、疑う余地はありません（私がその証明を理解したというわけではありませんが）。しかし、固定されたひとつの「真の平均」が存在しない場合はどうなのでしょう？

この話、突き詰めていけば非常に難しいところまでいってしまいます。けれどもそう深刻になる必要はないでしょう。絶対的な一点の期待値を求めようとするのではなく、幅を持ったものとして考える、そして検証結果より悪かったとしても利益が残るくらい余裕のある戦略作りを心がける。そのように考えることができるならば、十分に「役に立つ」レベルの知識だと思います。

統計学を知ることがエッジになるとは考えていますが、統計学で相場のすべてが解き明かせるとまでは思っていません。そこまで楽観的ではありません。統計学もひとつの道具、ゴルフクラブやバイオリンや人工衛星なんかと同じく、どれくらい役に立つかは使う人次第です。まずは日常のデータ整理のちょっとした効率化みたいなところからはじめて、だんだんと適用範囲を広げていく、というのがいいんじゃないでしょうか。